肯德爾等級相關係數 (Kendall tau rank correlation coefficient)

套路26: 肯德爾等級相關係數 

(Kendall tau rank correlation coefficient)

1. 使用時機: 肯德爾等級相關係數是用以反映兩組變數之間關係密切程度的統計指標。

2. 分析類型: 無母數分析(non-parametric analysis)。直接使用資料數值算統計叫parametric方法，把資料排序之後用排序的名次算統計叫non-parametric方法。

3. 肯德爾等級相關係數前提假設: 無。

4. 範例資料: 某研究餵食量對斑馬魚(zebrafish)存活的影響。在恆溫下，投入飼料X (mg)，斑馬魚存活比例Y的資料如下：

X (mg)	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55
Y (存活比)	1	0.95	0.95	0.9	0.85	0.7	0.65	0.6	0.55	0.42

餵食量與斑馬魚(zebrafish)存活有無線性關係?

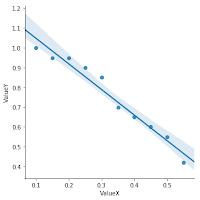
5. 畫圖看資料分佈:

v1 = [0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55]

v2 = [1, 0.95, 0.95, 0.9, 0.85, 0.7, 0.65, 0.6, 0.55, 0.42]

dat = {'ValueX':v1,'ValueY':v2}  # ValueX, ValueY是資料標題

import pandas as pd

df = pd.DataFrame(dat)

import seaborn as sb

from matplotlib import pyplot as plt

sb.lmplot(x = "ValueX", y = "ValueY", data = df)

plt.show()

# 灰色區域是回歸線的95%信賴區間。

6. 檢查資料是否為常態分布 (H₀:資料為常態分佈): 無母數分析無須檢查。

7. 使用Python計算肯德爾等級相關係數

方法:

v1 = [0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55]

v2 = [1, 0.95, 0.95, 0.9, 0.85, 0.7, 0.65, 0.6, 0.55, 0.42]

import scipy.stats

scipy.stats.kendalltau(v1, v2)

結果:

KendalltauResult(correlation=-0.9888264649460884, pvalue=7.772240795323109e-05)

肯德爾等級相關係數: -0.9888  p-value = 7.7722e-5 < 0.05

# 如計算結果p-value < 0.05，H₀: ρ = 0，不成立，X、Y有關。

# 如計算結果p-value > 0.05，H₀: ρ = 0，成立，X、Y無關。