測量資料的變異度 (Measures of Variability and Dispersion)
套路 3: 測量資料的變異度 (Measures of Variability and Dispersion)
什麼是資料的變異度與分散程度? 說白了就是變異數 (variance)、標準差 (standard variation)、標準誤差 (standard
error)或變異係數 (coefficient of variation)。
範圍(range)公式
如何使用Python計算範圍?
方法: 將上述計算公式寫成Python 程式
第一步: 資料 numStudent
= [58,57,54,59,53,56,58,59,60] #生物統計學歷年班級學生數
第二步: 程式
nRange = max(numStudent)
- min(numStudent)
nRange
# 結果: 7
變異數(variance) 公式
Population variance: 其中μ是母體(population)的算數平均數,Xi是第i個樣本,N是母體的樣本數。
Sample variance: 其中X橫槓是樣本(sample)的算數平均數,Xi是第i個樣本,n是抽樣的樣本數。
如何使用Python計算變異數?
方法一: 將上述計算公式寫成Python 程式
第一步: 資料 numStudent
= [58,57,54,59,53,56,58,59,60] #生物統計學歷年班級學生數
第二步: 程式
n = len(numStudent)
t1 = 0
for i in
range(n):
t1 = t1 + numStudent [i]
m = t1 / n
t2 = 0
for i in
range(n):
t2 = t2 + (numStudent [i] - m)**2
v = t2 / (n-1)
v
# 結果: 5.611111111111112
方法二: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
import
statistics
statistics.variance(numStudent)
# 結果: 5.611111111111111
方法三: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
from statistics
import variance
variance(numStudent)
# 結果: 5.611111111111111
標準差 (standard variation) 公式
Population STD:其中Xi是第i個樣本,N是母體的樣本數。
Sample STD: 其中Xi是第i個樣本,n是抽樣的樣本數。
如何使用Python計算標準差?
方法一: 將上述計算公式寫成Python 程式
第一步: 資料 numStudent
= [58,57,54,59,53,56,58,59,60] #生物統計學歷年班級學生數
第二步: 程式
n = len(numStudent)
t1 = 0
for i in
range(n):
t1 = t1 + numStudent[i]
m = t1 / n
t2 = 0
for i in
range(n):
t2 = t2 + (numStudent[i] - m)**2
std = (t2 /
(n-1))**(1/2)
std
# 結果: 2.3687784005919825
方法二: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
import
statistics
statistics.stdev(numStudent)
# 結果: 2.3687784005919825
方法三: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
from statistics
import stdev
stdev(numStudent)
# 結果: 2.3687784005919825
標準誤差 (standard error) 公式
Population standard error of mean: 其中s是母體標準差 (population standard deviation),n是樣本數。
Sample standard error of mean: 其中s是樣本標準差 (sample standard
deviation),n是樣本數。
如何使用Python計算標準誤差?
方法一: 將上述計算公式寫成Python 程式
第一步: 資料 numStudent
= [58,57,54,59,53,56,58,59,60] #生物統計學歷年班級學生數
第二步: 程式
n = len(numStudent)
t1 = 0
for i in
range(n):
t1 = t1 + numStudent[i]
m = t1 / n
t2 = 0
for i in range(n):
t2 = t2 + (numStudent[i] - m)**2
se = (t2 / (n *
(n-1)))**(1/2)
se
# 結果: 0.7895928001973276
方法二: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
import
statistics
std = statistics.stdev(numStudent)
n = len(numStudent)
se = std /
(n**(1/2))
se
# 結果: 0.7895928001973275
方法三: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
from statistics
import stdev
std = stdev(numStudent)
n = len(numStudent)
se = std /
(n**(1/2))
se
# 結果: 0.7895928001973275
變異係數 (coefficient of variation) 公式
Population CV: 其中μ是母體(population)的算數平均數,s是母體標準差 (population standard deviation)。
Sample CV: 其中X橫槓是樣本(sample)的算數平均數,s是樣本標準差 (sample standard
deviation)。
如何使用Python計算變異係數?
方法一: 將上述計算公式寫成Python 程式
第一步: 資料 numStudent
= [58,57,54,59,53,56,58,59,60] #生物統計學歷年班級學生數
第二步: 程式
n = len(numStudent)
t1 = 0
for i in
range(n):
t1 = t1 + numStudent[i]
m = t1 / n
t2 = 0
for i in
range(n):
t2 = t2 + (numStudent[i] - m)**2
std = (t2 /
(n-1))**(1/2)
cv = std * 100 /
m
cv
# 結果: 4.147666460180514
方法二: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
import
statistics
cv =
statistics.stdev(numStudent) * 100 / statistics.mean(numStudent)
cv
# 結果: 4.147666460180514
方法三: 使用Python 函數(function)
numStudent = [58,57,54,59,53,56,58,59,60]
import
scipy.stats
scipy.stats.variation(numStudent)
# 結果: 0.0391045744012486





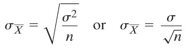






留言
張貼留言